Hypercube Network Topologies

Visualizing N-Dimensional Hypercubes

Three-Dimensional Hypercube		Four-Dimensional Hypercube
Five or more Dimensions... FORGET IT!

Constructing an N-Dimensional Hypercube

For dimension N+1, just create two hypercubes of dimension N, and connect analagous vertices.

3-D Hypercube

Dimensions:	N	3
Nodes:	2 ^N	2 ³ = 8
Links per Node:	N	3
Longest Path:	N	3

Four-Dimensional Hypercube

Node Numbering

Each node must differ from an adjacent node by at most one binary digit.

Three-Dimensional Hypercube

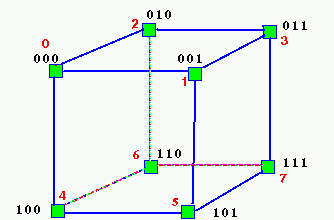Adjacent nodes differ by one binary digit.

Example in Node Numbering

Question: In a four-dimensional hypercube, what nodes connect to node 12?
Answer: 4, 8, 13, and 14

Solution:
First Convert to Binary: Node 12 = 1100 in Binary

Then apply the exclusive-OR (XOR) operation with a "1" digit in each of the four positions

1100 XOR 0001 = 1101 or 13
1100 XOR 0010 = 1110 or 14
1100 XOR 0100 = 1000 or 8
1100 XOR 1000 = 0100 or 4

The resulting values are the nodes that should link directly to node 12.

Routing Algorithm using XOR:

Use the Exclusive-Or operation again to determine which nodes will take the user closer to the destination:

Source XOR Destination => Which BITS need to be CHANGED.

Example: On Node #2 Trying to get to Node #7

Three Dimensional Hypercube

Source Node:
2 = 0 1 0
Destination Node:
7 = 1 1 1

XOR Operation:
0 1 0
1 1 1
------
1 0 1

Two Possible
First Moves:
3 = 0 1 1
6 = 1 1 0

After reaching either node 6 or node 3, the next move for either one should be node 7.

Two Possible Paths:
2 -> 6 -> 7
2 -> 3 -> 7

Traveling to node 0 moves one farther away from the destination.

Two Possible Simulation Techniques

A. Time-Step Approach Simple to implement but has problems

1. Increment Clock Variable by Time Step

2. Check to See if Anything Happens. If so, DO IT!

3. Go Back to #1.

B. Event-Driven Approach More sophisticated and more accurate

1. Make a List of Events and when they happen.

2. Sort the List to find Next Event. (Typically use a Heap.)

3. Update the Clock variable to the time the Event happens.

4. Do whatever the Next Event is.

5. See if this Event may cause some Other Events to happen. If so, put them in the Event List

6. Go Back to #2

Example Event-Driven Simulation

Consider the following example for a 3-D Hypercube:

Task Identification	Starting Node	Destination Node	Processing Time
A	2	7	1.2
B	4	7	2.3
C	5	7	3.1

Notes:

Only one task can occupy a node.
If a task tries to move to a busy node, it will try an alternative route.
If no paths will move a task closer to its destination, the task will be put into a WAIT state.
Nodes that have been blocked will send a WAKEUP MESSAGE to to waiting tasks.
(These messages will take a small, but measurable time such as 0.01 msec.)

Summary for Tasks A, B, and C
Task A: start on node 2, heading toward node 7, waits 1.2 msec on each node.
Task B: start on node 4, heading toward node 7, waits 2.3 msec on each node.
Task C: start on node 5, heading toward node 7, waits 3.1 msec on each node.
Any Task that cannot move must WAIT until it receives a WAKEUP message that will be received at Clock + 0.01 msec.

Example Scenario

Clock	Summary of Actions	Event List
Clock = 0.0 ( Initial)	Tasks A, B, and C are on nodes 2, 4, and 5 respectively and will wait appropriate times before moving.	A moves at 1.2 B moves at 2.3 C moves at 3.1
Clock = 1.2	Task A moves to node 3, NEXT EVENT (move) for A scheduled at 2.4 (current time + wait time)	B moves at 2.3 A moves at 2.4 C moves at 3.1
Clock = 2.3	Task B checks node 5, but discovers it is BLOCKED by C Task B moves to node 6, NEXT EVENT for B scheduled at 4.6	A moves at 2.4 C moves at 3.1 B moves at 4.6
Clock = 2.4	Task A moves from node 3 to node 7, NEXT EVENT for A at 3.6 (Note: A will sit blocking node 7 until clock=3.6)	C moves at 3.1 A moves at 3.6 B moves at 4.6
Clock = 3.1	Task C checks node 7, NODE BLOCKED (by A), cannot move (Task C goes into "sleep mode" and must WAIT until clock = 3.61, the time when the blocking task is finished and it receives WAKEUP message)	A moves at 3.6 C wakes at 3.61 B moves at 4.6
Clock = 3.6	Task A finishes and frees node 7, node 7 sends WAKEUP message to C at 3.61	C wakes at 3.61 B moves at 4.6
Clock = 3.61	Task C wakes up and moves to node 7 (it has been in WAIT mode since clock=3.1) Task C will sit there until Clock = 6.71 (3.61 current + 3.1 wait time)	B moves at 4.6 C moves at 6.71
Clock = 4.6	Task B tries to access node 7, but it is BLOCKED. B goes into "sleep mode" and must wait until clock = 6.72	C moves at 6.71 B wakes at 6.72
Clock = 6.71	Task C frees up node 7 and sends wake up call to B at clock = 6.72	B wakes at 6.72
Clock = 6.72	Task B wakes up and moves to node 7. Next event is at 9.02 when B is finished with node 7 and leaves the system.	B moves at 9.02
Clock = 9.02	Task B fished with node 7. Simulation is over and Event List is empty.	(empty)

Program Assignment

Your program should simulate the routing behavior of an N-Dimensional Hypercube where N can be easily changed from 3 to as many as 10 dimensions. This can be handled by having #define statements that reflect the number of dimensions as well as the number of nodes. By changing just these two parameters, the same program should work for the appropriate dimension. The program should also use an event-driven approach as described above.

The program should also reflect Object Oriented Programming (OOP) design. Although it is possible to generate the output of the simulation using a procedural approach without ever building objects such as the hypercube with tasks on the various nodes, and those nodes being aware of only thier own direct links, make sure your design utilizes strong OOP design skills.

Extra Credit Challenge:
Create a Graphical Representation of the simulation in OpenGL or Java.

Donald W. Hyatt: dhyatt@tjhsst.edu

Randy D. Latimer: rlatimer@tjhsst.edu

Phyllis T. Rittman: prittman@tjhsst.edu