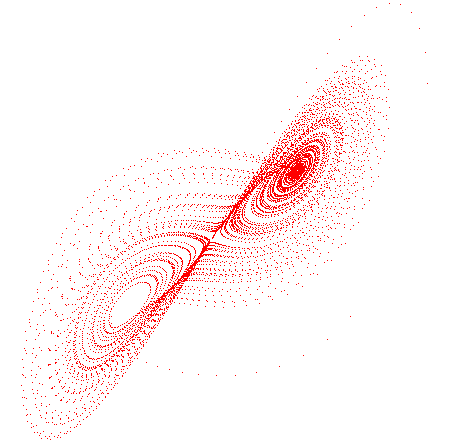
The Logistic Difference Equation is discussed in detail in your text, Chaos, Fractals, and Dynamics: Computer Experiments in Mathematics. It essentially relates a biology problem of a closed ecosystem such as a fish pond with a mathematical model. In the model, there is a finite number of fish in the pond, and the equation predicts the population of the next generation depending upon some reproduction rate. Interesting things happen as this equation is iterated over time, and different population rates are selected.
Depending upon the value of that growth rate, k, the following population dynamics
can be observed:
- The population converges to a single value, or attractor, after a period of time.
- The population does not converge, but bounces back and forth between two or more values. The point at which the split from one convergence point into two attractors is called bifurcation.
- The population goes into chaos, where each generation has a different number of fish than the previous, with little observable relationship to the previous one.
Variables
x - the percentage of fish in the pond, greater than 0 but less than 1.
k - the growth rate, greater than 0 but lesss than or equal to 4.
The Equation
xn+1 = k * xn * ( 1 - xn )
Graph of 100 Iterations of the Logistic Difference Equation for 0 < k < 4
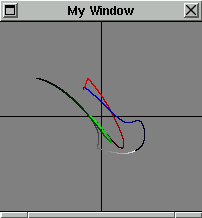
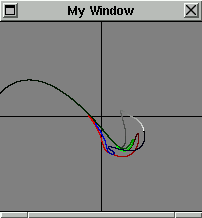
The Essentials for the Twist and Flip Algorithm:
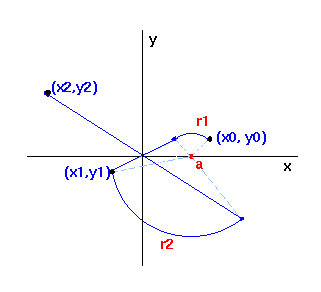For the twist and flip algorithm, a series of points is rotated r degrees around an
arbitrary position on the x-axis, point a. It is then flipped
diagonally through the origin to complete an iteration. The amount of rotation
is related to the distance, d, or the radius from a to that point.
The rotation function can be as unusual as one desires, but in the example
here, the farther away, the greater the rotation, although since the sine
and cosine values are in radians, the value of d is divided by 4.Variables for the Twist and Flip:
(x,y) - a point in the coordinate plane.
a - an arbitrary point on the x-axis
r - the amount of rotation, a function related to the distance d from a.
Equations:
d = sqrt((x - a)* (x-a) + y*y);
r = d/4.0;
xn = y * sin(r) + (a -x)* cos(r) - a;
yn = (a-x)* sin(r) - y * cos(r);
Iterating a Geometric Figure Using the Twist and Flip Algorithm
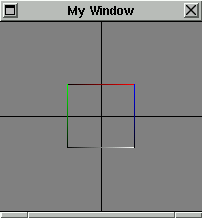
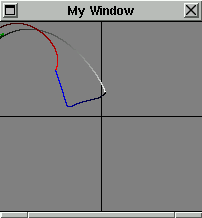
More Examples by Mark Hibbard
The Lorenz attractor is a famous set of equations that has been related to the study of dynamical systems such as weather prediction. The behavior of the system is very sensitive, and has generated the term, the "butterfly effect". The concept of the butterfly effect is that a butterfly flapping its wings in California could eventually have an effect on the weather of the east coast of the United States. The Lorenz attractor has a shape that looks like a butterfly at times, too.
Constants:
a = 10.0;
b = 28.0;
c = 8.0 / 3.0;
dt = 0.01;
Equations:
x1 = x + a * (y - x) * dt;
y1 = y + (x * (b - z) - y) * dt;
z1 = z + (x * y - c * z) * dt;
Graph of the Lorenz Attractor
