Supercomputer Applications
UNIT #4 - Iteration, Bifurcation, and Chaos
Introduction
In this unit, each student will develop interactive program in OpenGL that
experiments with one of the algorithms related to chaos and dynamical
systems. We want great diversity in this unit, so every student is expected
to select something different from the other students in their Imagining the
Future group.
Students will be graded on creativity, imagination, and appropriate use of
OpenGL concepts learned in this unit.
Detailed objectives are listed from a link at the bottom of
this page.
Chaos and Fractal Resources
The following reference materials will be helpful in understanding some
of the chaos and fractal algorithms that students may decide to investigate.
Select one of your choice, but preferably an algorithm that you have
not tried before.
Fractals and Graphics Program Examples
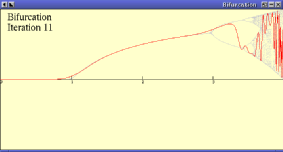
- Bifurcation Diagram
Drawing the Bifurcation Diagram for the Logistic Difference Equation
when 0 < k < 4.

-
Understanding Iteration
An interactive
program that shows the relationship
between an iterated function, the Logistic Difference Equation in the form of
a parabola, and the line y = x which can be used to show how
successive substitutions can be graphically obtained.

-
Orbits of Points
An interactive
program that shows the relationship
between the Mandelbrot Set and the orbit of points. Right mouse button
tells the imaginary number, left mouse button draws the orbit, the middle
mouse button erases the screen.
- Polynomial Equivalents
Demonstrating the resulting polynomial after each iteration for the logistic
difference equation.
Program Requirements for UNIT #4
The following page describes the assignments for UNIT #4. Review
them carefully, and when you have satisfied all the objectives, and have
completed a final web page presenting this unit, submit your code
and cover sheet to the teacher.



